And, Or, and the two KL-projections

Relating the two KL-projections to AND and OR

I discuss the difference between minimizing the KL-divergence with respect to the first and second argument, and will conclude that they correspond to AND and OR operations on distributions, respectively.

Oftentimes I see people wondering about the meaning of the two KL-projections:

\[\min_p D(p \| q) \qquad \text{versus} \qquad \min_p D(q \| p),\]

where of course, in the discrete case,

\[D(p \| q) := \sum_x p(x) \log \frac{ p(x) }{ q(x) }.\]

One popular intuitive explanation is that “the first projection finds the mode and the second the support”, motivated by depictions such as the following (from Manisha and Gujar, 2019)

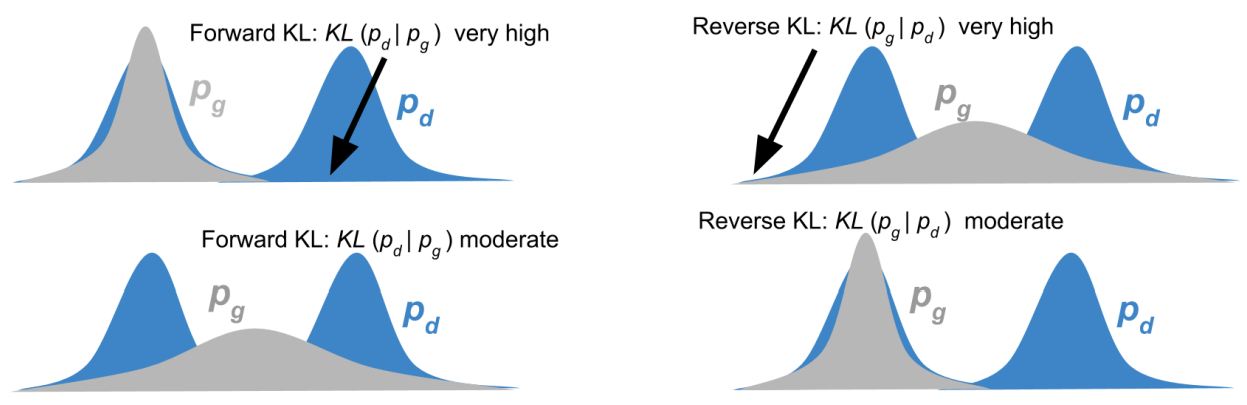
Personally, I find this explanation somewhat unclear and unsatisfying. I’ve grappled with this distinction since my PhD studies, while attempting to comprehend it from various perspectives, including information geometry. However, I was never truly happy with how the material was presented in the literature. I think the simplified explanation below, which took me years to arrive to, encapsulates a substantial amount of insight without relying on the complexities of information geometry. I hope you agree!

A tale of two coordinate systems

Understanding the distinction between the two projections solely by examining their application on two distributions can be quite challenging. Instead, a clearer grasp of the difference can be attained through the examination of mixture distributions. Let’s delve into this approach.

Linear mixture

Let’s say we have \(N\) distributions \(q_1, q_2, \ldots, q_N\) over a finite set \(\mathcal{X}\). Given a set of positive weights \(w_1, w_2, \ldots, w_N\) that sum up to one, their linear mixture is

\[q(x) = \sum_i w_i q_i(x),\]

The linear mixture expresses \(N\) mutually exclusive hypotheses \(q_i(x)\) that could be true with probabilities \(w_i\). That is, either \(q_1\) or \(q_2\) or … or \(q_N\) is true, with probability \(w_1\), \(w_2\), …, \(w_N\) respectively, expressing a disjunction of probability distributions.

Exponential mixture

Given a set of positive coefficients \(\alpha_1, \alpha_2, \ldots, \alpha_N\) (not necessarily summing up to one), their exponential mixture (a.k.a. geometric mixture) is

\[q(x) \propto \prod_i q_i(x)^{\alpha_i}.\]

It’s important to highlight that in order for the exponential mixture to yield a valid probability distribution, it has to be normalized.

The exponential mixture expresses \(N\) constraints \(q_i(x)\) that must be true simultaneously with precisions \(\alpha_i\). That is, \(q_1\) and \(q_2\) and … and \(q_N\) are true, with precisions \(\alpha_1\), \(\alpha_2\), …, \(\alpha_N\) respectively, expressing a conjunction of probability distributions.

Building conjunctions and disjunctions

So now that we’ve seen how to express conjunctions and disjunctions of distributions as exponential and linear mixtures respectively, we’ll try to find objective functions (or divergence measures, if you prefer) to build them.

Disjunctions: If I have a set of alternative hypotheses \(q_1(x)\) through \(q_N(x)\) which are true with probabilities \(w_1\) through \(w_N\) respectively, how divergent is \(p\) from this knowledge?

The answer is

\[\sum_i w_i D(q_i \| p).\]

That is, using the KL-divergences where \(p\) is the second argument. Indeed, the minimizer is precisely the linear mixture:

\begin{equation} \label{eq:build-linear} \arg\min_p \sum_i w_i D(q_i | p) = \sum_i w_i q_i(x). \end{equation}

Conjunctions: If I have a set of simultaneous constraints \(q_1(x)\) through \(q_N(x)\) with precisions \(\alpha_1\) through \(\alpha_N\), how far off is \(p\) from this knowlegde?

The answer is

\[\sum_i \alpha_i D(p \| q_i).\]

That is, using the KL-divergences where \(p\) is in the first argument. And in fact, the minimizer is precisely the exponential mixture:

\begin{equation} \label{eq:build-exponential} \arg\min_p \sum_i \alpha_i D(p | q_i) \propto \prod q_i(x)^{\alpha_i}. \end{equation}

Equations \eqref{eq:build-linear} and \eqref{eq:build-exponential} form the core of my argument. Basically, we have found a relation between the two KL-projections and the two logical operators and and or. The two KL-divergences then measure the divergence of \(p\) from a conjunction and disjunction, respectively.

Final thoughts

As a final comment, I’d like to point out the connection to the Bayesian framework. Let’s consider hypotheses \(h \in \mathcal{H}\) with i.i.d. likelihoods \(q(x|h)\) over \(\mathcal{X}\) and priors \(q(h)\).

Prediction: The first step is to build the predictor. Since we believe that one and only one hypothesis is true, then we take the disjunction over the likelihoods (or expert predictors), where the weights are given by the prior probabilities:

\[\arg\min_{p(x)} \sum_h q(h) D\big(q(x | h) \big\| p(x) \big) = \sum_h q(h) q(x|h).\]

The resulting estimator \(\sum_h q(h) q(x \mid h)\) is the Bayesian estimator.

Belief update: The second step is to understand how to update our beliefs after making an observation. It turns out that an observation is a constraint on the prior beliefs, i.e. we obtain the posterior through a conjunction between the prior and the likelihood function. If \(\dot{x}\) is our observation, then the conjunction is

\[\arg\min_{p(h)} \big\{ \alpha D\big(p(h) \big\| q(h)\big) + \beta D\big(p(h) \big\| q(\dot{x}|h)\big) \big\} \propto q(h)^\alpha q(\dot{x}|h)^\beta.\]

In this operation we use precisions equal to \(\alpha=\beta=1\) so that the result is proportional to \(q(h)q(\dot{x}|h)\). We can easily verify that the right hand side is indeed the Bayesian posterior after normalization.

Notice how building the predictor involves taking the disjunction of distributions over the observations \(x\), while computing the posterior amounts to computing the conjunction of functions over the hypotheses \(h\). In doing so, we interpret the likelihood as two different functions: in the disjunction, it is regarded as a function of \(x\) whereas in the conjunction it is a function of \(h\).

Thus, it turns out that sequential predictions can be regarded as an alternation between OR and AND operations, first to express our uncertainty over the hypotheses, and second to incorporate new evidence, respectively.